Binary Search

Introduction

Binary Search is a searching algorithm for finding the target element's position in a sorted array.

It follows the Divide and Conquer approach in which the array is divided in two halves.

Binary Search can be implemented only on sorted array. If the array is not sorted , we need to sort them first.

Working of Binary Search

Binary Search algorithm can be implemented in two ways :

1. Iterative Method

2. Recursive Method

The general approach for both methods are discussed below :

1. The original array in which sorting is to be performed is

2. Let x = 4 be the target element to be searched. Now using the Two Pointer method , set the pointers on the lowest and the highest position of the array respectively.

3. Find the middle element of the array i.e mid.
By using the formula mid = low + (hi- low) / 2

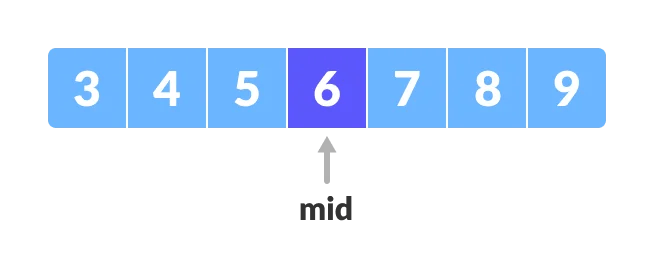
We are not using mid = low + high / 2 because this can give bugs when the array is too big.

4. If target element x == mid , then return the mid index.

5. Check if the element x is greater than the mid element i.e x > mid
then move the low pointer to the mid + 1 element . This can be done by low = mid + 1

6. Else, check the x is smaller than the mid element i.e x < mid
then move the high pointer to mid - 1 element. This can be done by high = mid - 1

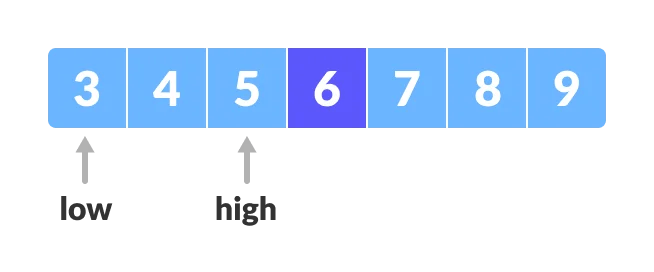
7. Repeat steps 3 to 6 until low meets high.

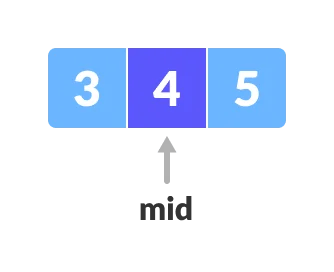
8. x = 4 is found

If target element x not found, It means x doesn't exist in the array.
Simply return -1.

Code (in Java) :

• Iterative Method

public class BinarySearch {
    public static void main(String[] args) {

        int[] arr = {3, 4, 5, 6, 7, 8, 9};
        int target = 4;
        System.out.println(binarySearch(arr,target));
    }

    // binary search
    static int binarySearch(int[] arr, int x) {
        int low= 0;
        int high= arr.length - 1;

        while (low <= high) {

            // find the middle element
            int mid = low + (high - low) / 2;

            if (x > arr[mid]) {
                low = mid + 1;

            } else if (x < arr[mid]) {
                high = mid - 1;

            } else {
                // return mid
                return mid;
            }
        }
        // if target not found 
        return -1;
    }
}

• Recursive Method

public class BinarySearchRecursion {

    public static void main(String[] args) {
        int[] arr = {3, 4, 5, 6, 7, 8, 9};
        int target = 4;
        System.out.println(binarySearch(arr ,x ,0 ,arr.length-1));
    }

    static int binarySearch(int[] arr, int x, int low, int high){

        // base condition
        if(low > high){
            return -1;
        }
        int mid = low + (high - low) / 2;

        if(x == arr[mid]){
            return mid;
        }
        if(x > arr[mid]){
            return binarySearch(arr, x, mid + 1, high);   // recursive call
        }
        return binarySearch(arr, x, 0, mid - 1);    // recursive call
    }
}

Binary Search Complexity

Time Complexity

• Best Case : O(1)
• Average Case : O(log N)
• Worst Case : O(log N)

Space Complexity

Space Complexity of Binary Search is constant i.e O(1).